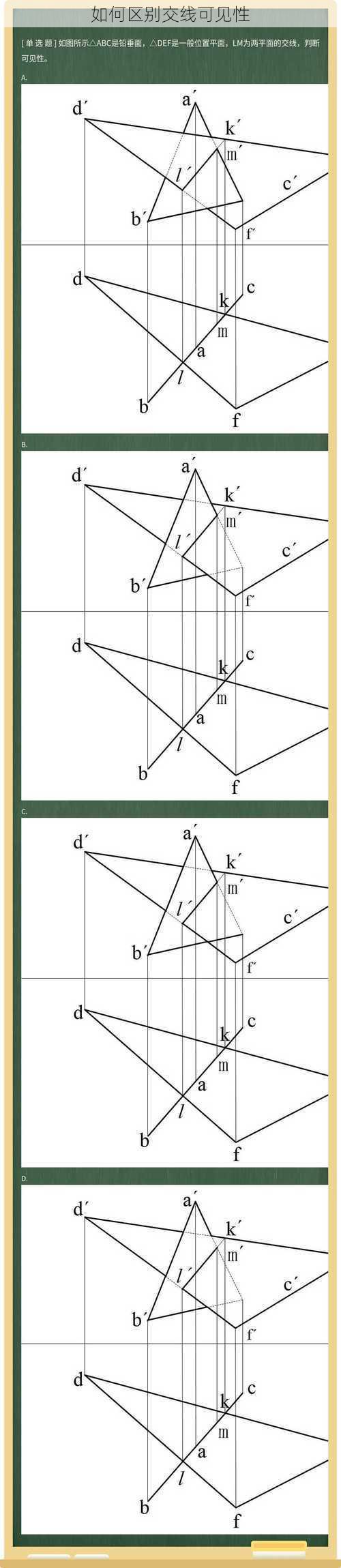
如何区别交线可见性

在二维图形中，两条直线的交点称为交点。当这两条直线都是可见的，或者都是不可见的，那么这个交点就是可见的；如果其中一条直线是隐藏线，那么这个交点就是不可见的。在三维图形中，两个平面的交线称为交线。当这两个平面都是可见的，或者都是不可见的，那么这个交线就是可见的；如果其中一个平面是隐藏面，那么这个交线就是不可见的。

在机械制图中，为了表示机件的内部形状，常用虚线表示不可见的结构。在同一张图纸上，虚线与实线的交点应是可见的。但在实际画图中，由于种种原因，虚线与实线的交点可能会出现不可见的情况。下面介绍几种判断交线可见性的方法。

利用积聚性判断

当直线或平面处于特殊位置时，它们的积聚性会使交点的可见性变得明显。

1. 直线处于投影面垂直线上时，积聚成一点，交点可见。

2. 直线处于投影面平行线时，积聚成一条直线，交点可见。

3. 平面处于投影面垂直面时，积聚成一条直线，交点可见。

4. 平面处于投影面平行面时，积聚成一个点，交点可见。

利用辅助平面法判断

当直线或平面的积聚性无法确定交点的可见性时，可以通过作辅助平面来判断。

假设有两条直线 AB 和 CD，它们的交点为 I，我们过点 I 作一个辅助平面 P。如果辅助平面 P 与直线 AB 和 CD 都相交，那么交点 I 就是可见的；如果辅助平面 P 只与直线 AB 或 CD 相交，那么交点 I 就是不可见的。

利用重影点法判断

当直线或平面在投影面上的投影重合时，称为重影点。利用重影点法可以判断交点的可见性。

假设有两条直线 AB 和 CD，它们在 H 面上的投影重合，称为重影点。我们取正面投影面 V，过点 I 作一条垂直于 H 面的直线 MN。如果直线 MN 与直线 AB 的正面投影 a'b'相交，与直线 CD 的正面投影 a''c''不相交，那么交点 I 就是可见的；如果直线 MN 与直线 AB 的正面投影 a'b'不相交，与直线 CD 的正面投影 a''c''相交，那么交点 I 就是不可见的。

利用虚实线法判断

在同一张图纸上，虚线与实线的交点应是可见的。当虚线与实线相交时，我们可以根据虚线的虚实来判断交点的可见性。

如果虚线是实线的延长线，那么交点是可见的；如果虚线不是实线的延长线，那么交点是不可见的。

判断交线可见性的方法有很多种，我们可以根据具体情况选择合适的方法。在实际画图中，我们应该仔细分析图形的特点，灵活运用各种方法，以保证图形的表达清晰、准确。